4.0 Assessment of Sampling Plans

VSP provides multiple displays for allowing you to assess a sampling plan. VSP calls the displays Views. You can view a representation of the sampling locations on the map entered into VSP, view a graph of the performance of the design, look at a report that summarizes the key components of the design (such as number of samples, size of sampling area, cost, probabilities associated with the problem, assumptions, and technical justification), see a listing of the coordinates of each sampling location.  For three dimensional sampling areas such as buildings and rooms, you can view a 3-D display of the entire building, and you can also toggle through individual rooms choosing from several ways to display the rooms. There also is an option which allows for displaying several of these views in different windows simultaneously. This section describes each of these views and discusses how you can use the views to assess the VSP sampling plan.

There are two ways to select/change views:

• Press one of the display buttons in the middle of the tool bar (MAP VIEW, GRAPH VIEW, REPORT VIEW, COORDINATE VIEW, 3D VIEW).  If you are working with rooms, the ROOM VIEW may also be used.  The QUAD WINDOW button creates 4 separate windows for displaying multiple views simultaneously.

• From the main menu select View > Map (or Graph, Report, Coordinate, Room, 3D)

4.1 Display of Sampling Design on the Map:  MAP VIEW button or View > Map

In Section 2.2, we described how to set up a Map. In Section 2.3, we described how to set up a Sample Area. In Section 3.1, we described how to select a Type of Sampling Plan. In this section, we find out how to view the results of the sampling design we have just developed and displayed on the map.

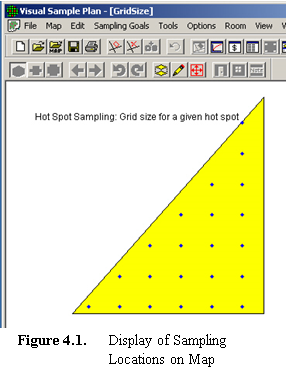
In Figure 4.1, we see the display of a simple triangle we drew as our map and selected the entire triangle as our Sample Area. This is available in the file GridSize.vsp, which is included with the VSP program.

We then selected from the main menu Sampling Goals > Locate Hot Spots > Assume no false negative errors. We selected the Probability of Hit to be 90% and selected a Square grid. We indicated that we wanted to detect a circular hot spot by selecting a Shape of 1.0 and a Radius of 4.0 feet.  We press Apply, and when we return to the map (View > Map) we see the 22 samples VSP calculated as required to meet the sampling goal displayed. Each time we press Apply, we refresh the map display with a new set of random-start sampling locations.

4.2 Display of Cost of Design

In Section 5.4, we describe how to enter costs. For most sampling designs, Total Cost (per unit plus fixed costs) is tallied and displayed on the same screen where we enter the per-unit costs-under the Costs tab on the dialog box used for entering design parameters.  Cost information is also usually available in the Report View (View > Report). Reports are discussed in detail in Section 4.4.

4.3 Display of Performance of Design:  GRAPH VIEW button or View > Graph

VSP provides a display of the Performance of the Design for all of the sampling plans that result from sampling goals where a quantitative decision criterion is supplied. For some sampling goals where the only criterion the plan must meet is to minimize the variance of the estimate, minimize cost of the estimate, or to calculate a probability, there is little to graph in terms of the performance of the design. For such sampling goals, selecting View > Graph brings up a blank graph titled "No Graph". For some designs, such as "Detect a Trend", the Graph view will display a graph of actual data after it is entered into the Data Analysis page of the design dialog.

For the sampling goals that do specify decision error rates or have confidence bounds on the estimates, VSP provides a graph of the performance of the sampling design that has just been created. Each sampling goal, or problem type, has a performance display tailored to it. Each graph tries to show the relationship between some parameter of the sampling design and how effective that design is at achieving the decision criteria. Once a Sampling Goal has been selected, the DQO inputs are entered on the dialog box input screen, and the Apply button is pressed to apply the design to the Sample Area, the display of the performance can be seen by pressing the GRAPH VIEW button on the tool bar or selecting View > Graph from VSP's main menu.

The following sections describe the major displays available for various types of problems. Displays not described are variants of those presented. Some of the graphs associated with unique sampling designs, such as Sequential Sampling, have been described in earlier sections, e.g., Graph View of Sequential Sampling (Figure 3.8), found in Chapters 3 and 2. Graphs for UXO-related Sampling Goals are discussed in Chapter 7. 

4.3.1 Performance of Design for Sampling Goal:  Compare Average to a Fixed Threshold

The display for the goal of comparing an average to a fixed threshold (i.e., the Action Level) is a graph of the probability of deciding the true mean of the sample area is greater than or equal to the Action Level on the vertical (y) axis as opposed to a range of possible true mean values on the horizontal (x) axis. Figure 4.2 is the Decision Performance Goal Diagram (DPGD) described in EPA's QA/G-4 guidance (EPA 2000a, pp. 6-7 - 6-11).  The document can be downloaded from the EPA at: http://www.epa.gov/quality/qa_docs.html. Notice how the graph changes as we alternate the null hypothesis between "Assume Site Dirty" to "Assume Site Clean."

The solid vertical red line is positioned at a true mean value of 10, which corresponds to the Action Level. The area in gray hash marks is the gray region shown here from 8 to 10 and input as a delta (width) of 2. The two dashed blue lines that extend from the y-axis to the x-axis mark the two types of decision error rates, alpha, set here at 5%, and beta, set here at 10%. Recall that Alpha is the probability of rejecting the null hypothesis when it is true (called a false rejection decision error), and beta is the probability of accepting the null hypothesis when it is false (called a false acceptance decision error). The error rates along with

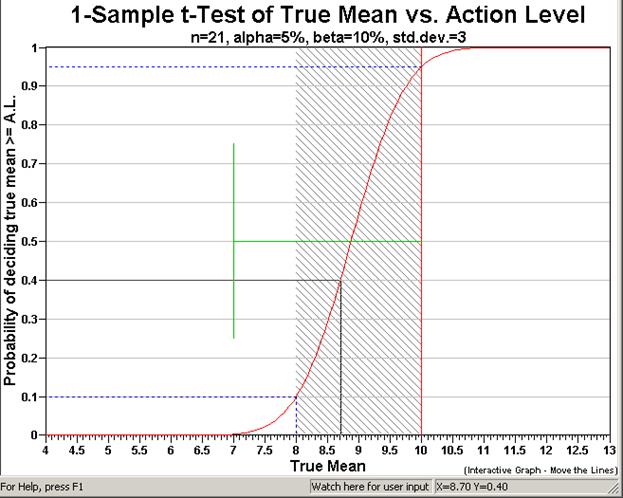
Figure 4.2.     Decision Performance Goal Diagram for Null Hypothesis:  True Mean >=Action Level for Comparing Mean vs. Action Level

the user-supplied standard deviation of 3 and the VSP-calculated sample size n=21 are shown on the second row of the title. We also see in the title that we are using the sample size formula for the one­ sample t-test.

The green vertical line marks off one standard deviation (3) from the action level. This mark allows the user to visually compare the width of the gray region to how variable, on average, we expect individual observations to be about the mean (definition of standard deviation). The sliding black lines (cross hairs) that move on the graph when the mouse is moved are provided to facilitate reading the x, y values off the graph. This cross-hair feature can be turned off or on by choosing Options > Graph > Display Cross Hairs.

Most of the parameters displayed on the DPGD can be changed interactively by moving the lines on the graph, rather than having to change the values in the input dialog box.  Table 4.1 describes the interactive features.

Table 4.1.   Interactive Graph Features

As you change these parameters, you can see the new value of the parameter on the bottom status bar after "watch here for user input." You will notice that changing these values on the graph also changes these values on the other displays:  the sampling design is modified in the report view, new samples are placed on the map view, and updated sample location information is listed in the coordinate view.

Right-clicking anywhere in the graph brings up a pop-up menu. The options in the menu are described in Table 4.2. This pop-up menu provides quick access to the menu choices available from the main menu under Options > Graph. One of the options is to view the complement of the Decision Performance Goal Diagram, which is referred to as the "Operating Characteristic" Curve.  We select this option and the OC curve is shown in Figure 4.3. Note that the Y-axis is now labeled, "Probability of making the correct decision".

Table 4.2.   Graph Options Menu Commands

When the null hypothesis is stated as H₀:  True Mean = Action Level (Site is Dirty), the gray region is on the left side of the Action Level.  However, when the null hypothesis is stated as H₀: True Mean = Action Level (Site is Clean), the gray region is on the right side of the Action Level. In practical terms, when we assume a site is dirty, the majority of the decision errors will occur for clean sites with true means just below the Action Level. On the other hand, when we assume a site is clean, the majority of decision errors will occur for dirty sites with true means just above the Action Level.

The DPGD graph in Figure 4.3 is telling us that for the "Site is Dirty" null hypothesis,

• Very clean sites will almost always result in sets of random sampling data that lead to the decision "Site is Clean."

• Very dirty sites will almost always result in sets of random sampling data that lead to the decision "Site is Dirty."

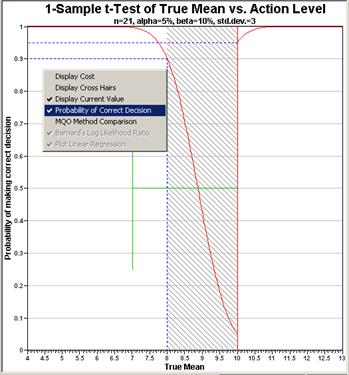
Figure 4.3.     Graph of Probability of Making Correct Decision

What we may not know intuitively is how our choice of the null hypothesis affects decisions near the Action Level. The graph in Figure 4.3 also is telling us

• Clean sites with true means just below the Action Level will lead to mostly incorrect decisions.

• Dirty sites with true means just above the Action Level will lead to mostly correct decisions.

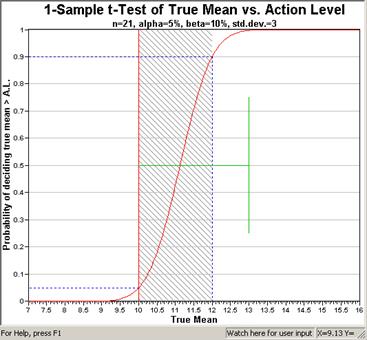
Figure 4.4.     Decision Performance Goal Diagram for Null Hypothesis:  True Mean <=Action Level for Comparing Mean vs. Action Level

However, when we reverse the null hypothesis and state it as H₀:  True Mean = Action Level, i.e., assume "Site is Clean," we see in Figure 4.4 that the gray region where the majority of decision errors occur shifts to the right side of the Action Level.  Sites that are dirty now lead to the majority of decision errors.  Also note that alpha is now defined for values less than the action level, while beta is defined for values above the upper bound of the gray region.

You should carefully study EPA's QA/G-4 guidance document (EPA 2000a, especially pp. 6-1 to 7-6) to better understand how to use VSP to balance the choice of null hypothesis, decision error rates, width of the gray region, total sampling costs, and costs of incorrect decisions.

4.3.2 Performance of Design for Sampling Goal:  Construct Confidence Interval on the Mean

The display for assessing a confidence interval for a mean differs somewhat from that for comparing an average to a threshold because this is an estimation problem, not a testing problem. As such, there is only one type of decision error rate, alpha. Shown in Figure 4.5 is the Performance Design for a problem where the user specified the width of the confidence interval as 1.0, the standard deviation as 3, and a desired 95% one-sided confidence interval on the mean. We are using a one-sided confidence interval (vs. a two-sided) because we are concerned only about values that exceed the upper bound of the confidence interval, not values both above the upper bound and below the lower bound. This is consistent with problems in which the mean to be estimated is average contamination, so we are not concerned about values below the lower bound of the confidence interval.

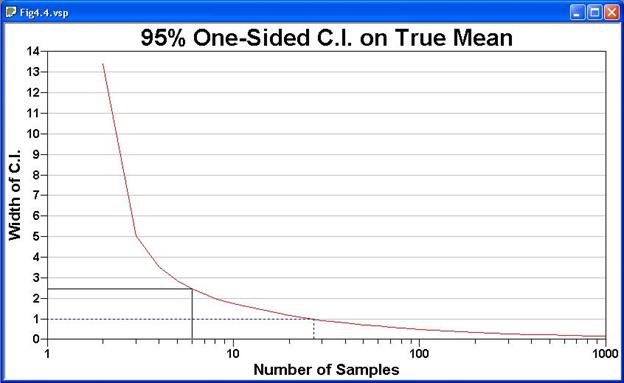
Figure 4.5.     Decision Performance Graph for One-Sided 95% Confidence Interval

VSP calculated that a sample size of 27 was required. The performance graph is a plot of possible confidence interval widths vs. number of samples for the problem specified. The dashed blue line terminates at the y-axis at a confidence interval width of 1.0, as specified by the user, and at the x-axis at the recommended minimum sample size of 27.

The solid black line is a locating aid you can slide up and down the graph to easily read the trade-offs between increased width of the confidence interval and increased number of samples. In VSP, the x-axis value (number of samples) and the y-axis value (width of confidence interval) for the current solid black line are located in the status bar below the Graph view.

4.3.3 Performance of Design for Sampling Goal:  Comparing a Proportion to a Fixed Threshold

The sampling design assessment display for comparing a proportion to a fixed threshold is a graph of the DPGD for the DQO inputs supplied. Note:  If the appropriate statistical test is used, the test is designed to achieve the level of significance, or alpha. It is beta and the power of the test (1-beta) that are affected by sample size.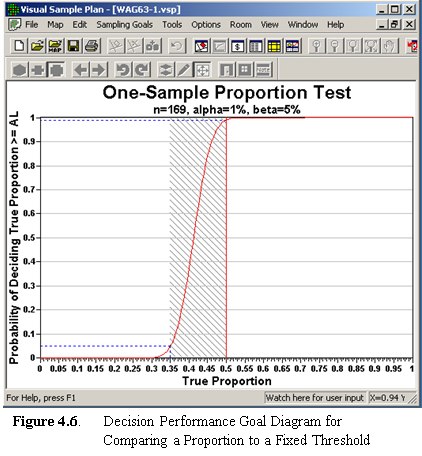

For this sampling goal, there is no clear distinction between "Site Dirty" and "Site Clean," depending on how the null hypothesis is formulated. If the proportion we are talking about is the proportion of 1-acre lots in a building development that have trees, then exceeding a threshold would be a "good thing." However, if the proportion is the proportion of acres that have contamination greater than 10 pCi, then exceeding the threshold would be a "bad thing."  Alpha and beta are still defined as false acceptance and false rejection rates, but the user must formulate the hypotheses and select limits on the error rates consistent with the goals of the project and which type of error is most important to control.

In the example in Figure 4.6, the null hypothesis was set to True Proportion = Given Proportion.  As such, beta is the probability of deciding the proportion exceeds the threshold when the true proportion is equal to or less than the lower bound of the gray region. For this problem, we set alpha to 1% and beta to 5%, and the lower bound of the gray region to 0.35 (i.e., width of gray region=0.15). The proportion we want to test against (Action Level) is 0.5. This Action Level is the most conservative. That is, the largest number of samples are needed to differentiate a proportion from 0.5 (vs. differentiate a proportion from any other percentage). 

4.3.4 Performance of Design for Sampling Goal:  Compare Average to Reference Average

The sampling design performance display for comparing the true means of two populations when the assumption of normality can be made is a graph of the probability of deciding if the difference of true means is greater than or equal to the specified difference (Action Level) vs. various differences of true means. This graph is similar to the Decision Performance Goal Diagram discussed in Section 4.3.1, but this time we are dealing with two populations, and the x-axis is a range of possible differences between the two population means.

The graph shown in Figure 4.7 is for H₀: Difference of True Means = Action Level.  We revert back to the notion that this null hypothesis implies a " Dirty Site" condition. If the action level is a positive number, we would classify the site as greater than background or "Dirty."  For this problem, the specified difference of the two means (Action Level) is 5, the width of the gray region is 2, alpha=5%, beta=10%, and the estimated common standard deviation=3.

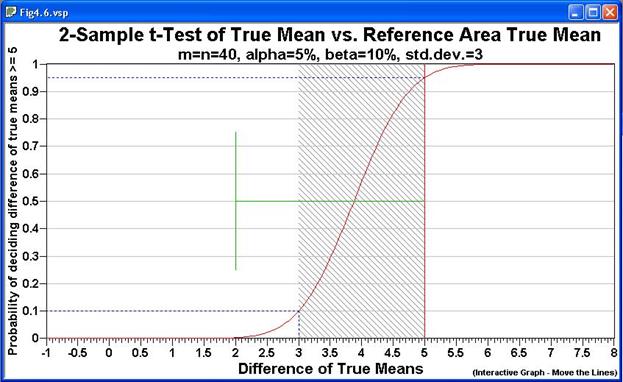
Figure 4.7.     Decision Performance Goal Diagram for Comparing a Sample Area Mean to a Reference Area Mean

Note:  The standard deviation is the average expected difference between the individual units in a population and the overall mean for that population. It is assumed that both populations (Sample Area and Reference Area) have the same standard deviation. The graph is labeled "2-Sample t-Test" because it is assumed that the two-sample t-test will be used as the statistical test.

The title of Figure 4.7 shows that we need to take 40 samples both in the Sample Area and 40 samples in the Reference Area. The probabilities of deciding the Sample Area is 5 or more units (pCi/g, ppm, etc.) above the Reference area are plotted against the true differences in means. The standard deviation is shown as the green line at a distance of 3 from the Action Level.

When the assumption data are not required to be normally distributed is made, we can see from the pull-down menu lists under Sampling Goals that a non-parametric statistical test is proposed - the MARSSIM WRS (Wilcoxon rank sum) test.

The Decision Performance Goal Diagrams for the MARSSIM WRS is similar to the DPGD for the parametric two-sample t-test. In Figure 4.8, we see the DPGD for the MARSSIM WRS test using the same inputs as the problem in Figure 4.7. The difference of true means or medians is plotted on the x-axis, and the probability of deciding the difference is equal to or greater than the action level of 5 is shown on the y-axis. For the MARSSIM formulation of the WRS test, the action level is the Derived Concentration Guideline Level for average concentrations over a wide area (DCGLw). The lower bound of the gray region is the difference in means or medians where we want to limit the beta error.

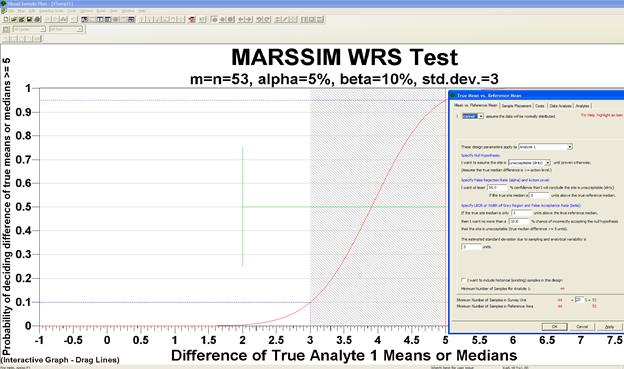
Figure 4.8.     Decision Performance Graph for Comparing a Sample Area Mean to a Reference Area Mean (Nonparametric Version, MARSSIM WRS)

Shown in Figure 4.8, the input dialog for the MARSSIM WRS test allows the user to supply a percent overage to apply to the sample size calculation. MARSSIM suggests that the number of samples should be increased by at least 20% to account for missing or unusable data and for uncertainty in the calculated values of the Sample Size, n. With the extra 20%, the sample size now becomes 53 samples required in both the Sample Area (i.e., Survey Unit or Study Area) and Reference Area.

4.3.5 Performance of Design for Sampling Goal for Hot Spot Problem

The Decision Performance Goal Diagram for the hot spot problem is a graph of number of samples on the x-axis and the probability of hitting a hot spot of a specified size on the y-axis. The heading of the performance graph lists the size of the hot spot and the size of the sample area. The trade-off displayed is that by increasing the number of samples (i.e., a tighter grid spacing and hence the higher cost), and/or changing the grid type (say from square to triangular), there is a higher probability of hitting the hot spot with one of the nodes on the grid.  This is almost a straight-line relationship until we get into larger sample sizes, and then the efficiency is diminished.

Returning to the problem we laid out in Section 4.1, for the sampling goal of Sampling Goals > Locating a Hot Spot > Assume no false negative errors, the graph is shown in Figure 4.9. This graph is for the 1130.84 ft² Sample Area shown in Figure 4.1 and for finding a 4-ft round hot spot. The graph shows the desired input of 90% probability of hitting the circular hot spot of radius 4 ft. and the 22 samples required to achieve this. The DPGD for this problem is a graph of the % probability of a hit on the Y axis vs. the number of samples using a square grid on the X axis. The user can move the cursor along the curve to read off alternative combinations of probability of a hit for different samples sizes (i.e., grid size).

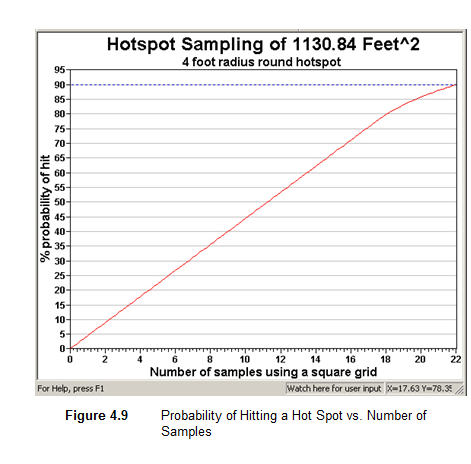VSP may place a slightly different number of sampling points (nodes) on a map than the exact number calculated. The difference between the calculated number of samples and the number of samples placed on the map is 1) grid edge effects, 2) adding judgment samples, or 3) selecting or unselecting sample areas. Repeatedly pressing the Apply button from the dialog box will select a different random starting point for the grid and may change the number of samples that will fit in the sample area.

The probability of hit is a geometric relationship between the grid spacing and the hot spot size and shape. The probability of hit is not a function of number of samples. On the graph, however, grid spacing is translated to the number of samples on a theoretical sampling area. The number of theoretical samples is shown on the graph because it is a more meaningful metric for the user than grid spacing. The dashed blue line on the performance curve shows the number of samples that fit on the actual sample area given the starting point.  The report also lists the actual number of samples placed on the map.

Important note:  Regardless of where the dashed blue line occurs on the graph, the probability of a hit for your sampling design is the one you specified and is shown on the sampling goal dialog. This is true because the probability of a hit is a geometric relationship between the grid spacing and the hot spot size and shape.

Deselecting the Random Start on the dialog box removes the random assignment of the grid and keeps the grid fixed with each repeated hit of the Apply button, keeping the same sample size.

4.3.6 Performance of Design for Sampling Goal of Compare Proportion to a Reference Proportion

The graph for displaying the performance of the design for comparing a proportion to a reference proportion is similar to the comparison of two population means (see Figure 4.7). As such, the difference between the two true proportions is shown on the x-axis, and the probability of deciding that the difference between the two true proportions is greater than a specified difference (i.e., the Action Level) is shown on the y-axis. The two proportions being compared could be, say, the proportion of children with elevated blood lead in one area compared to the proportion in another area, or it could be the percentage of 1-m squares within an acre that have contamination greater than 1 ppm of dioxin. The comparison might be to compare the amount of contamination (stated as a percentage remaining at a site after it has been remediated) to a background or reference area. Using the naming convention in EPA (2000b, pp. 3-27 - 3-31), the site (also called the survey unit, Sample Area) is Area 1, and the reference or background area is Area 2. The document can be downloaded from the EPA site:  http://www.epa.gov/quality/qa_docs.html.

In Figure 4.10, we see the inputs from the dialog box along with the Decision Performance Goal Diagram. The example has as the null hypothesis "no difference between site and background," or Ho:  P1 - P2 = 0. The two estimated proportions are required to calculate the standard deviation for the pooled proportion used in the sample size formula.  With this formulation, the specified difference (Action Level) is 0, and the false acceptance error rate (beta=5%) is set at the difference of P1 - P2=0.10. Thus, 0.10 is the upper bound of the gray region, which VSP requires to be greater than the Action Level. When the null hypothesis is changed to Difference of Proportions = Specified Difference, the lower bound of the gray region is less than the action level.

The graph in Figure 4.10, labeled the Two-Sample Proportion Test, lists the inputs of alpha, beta, and the two estimated proportions in the heading line. The S-shaped curve shows that for larger differences in the true proportions, the probability of correctly deciding the difference exceeds the Action Level increases. This is intuitive because the greater the difference between two populations, the easier it is to correctly distinguish that difference from a fixed threshold (Action Level).

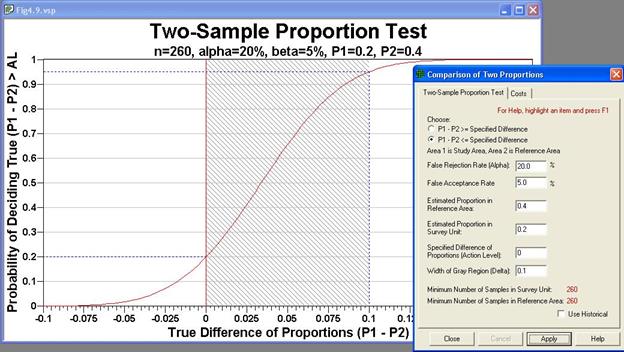
Figure 4.10.   Decision Performance Goal Diagram for Comparing a Sample Area Proportion to a Reference Area Proportion.  Input dialog box for design shown as insert.

4.3.7 Performance of Design for Sampling Goal of Establish Boundary of Contamination

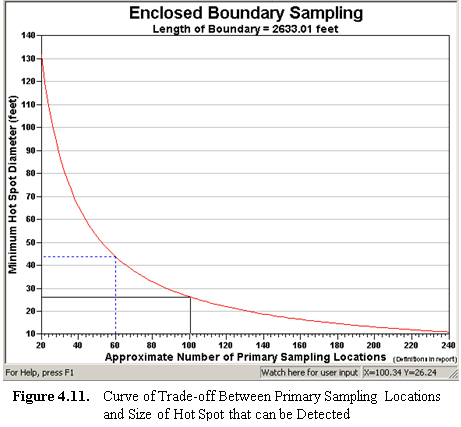
In Figure 4.11 we see the performance of the sampling design defined by the inputs shown in Figure 3.36 applied to the Sample Area of the large "oval" in the Millsite.dxf file (see Map View in Figure 3.38). This problem is for the Enclosing Boundary. In order to have a 95% confidence of finding a hot spot of diameter of 45 ft, we need 12 segments.  This dictates we need 60 Primary Sampling Locations (12 x 5=60).  The relationship between diameter of hot spot and number of primary sampling locations is shown in the dashed blue line positioned on the performance curve shown in Figure 4.11. The dashed line shows the current number of Primary Sampling Locations for this design (n=60), which may differ from the optimum number because of rounding and bump-out effects. We can see from the cross hairs positioned on the performance curve (right-click on graph, and toggle the Display Cross Hairs to "on"), that if we expand our Primary Sampling Locations to 100, we could detect a hotspot of diameter 27 ft. with the sample level of 95% confidence.

The sample type of graph is produced for the Open Boundary Sampling Problem.

4.4 Display of the Report

One of the most valuable outputs from VSP is the Report that is generated for each application of a Sampling Design to a Sample Area. The Report View for a sampling design is available by either selecting the REPORT VIEW button on the toolbar, or by selecting View > Report from the main menu. The only Sampling Goals that do not produce Reports are Non-statistical sampling approaches and Comparisons of two proportions. 

The Report provides the VSP user with a complete documentation of the sampling design selected. The report includes:

• statement of sampling objective,

• the assumptions of the design,

• sample size formula,

• inputs provided by the user,

• summary of VSP outputs including sample size and costs,

• list of samples with their coordinates and labels,

• map with sample locations identified,

• Performance Goal Diagram,

• Peer-reviewed technical references for designs and formulas,

• technical discussion of the statistical theory supporting the sampling design and sample size formula.

The reports are suitable for incorporation into a quality assurance project plan or a sampling and analysis plan. The report for some of the sampling designs include:

• recommended data analysis activities for how data should be used in the appropriate statistical test to make a decision,

• insight into options presented in the Input Dialog Box,

• sensitivity tables showing how sample number changes as input parameters change, and

• extended statistical discussions and support equations.

Some of the output from VSP, for some designs, is viewable only within the report. VSP users can use the information in the Report as an additional source of Help.

A few selections from the report for the selection Sampling Goals > Compare Average to a fixed threshold, with can assume the data will be normally distributed and ordinary sampling selected, are shown in Figure 4.12. Each time VSP calculates a new sample size, changes VSP input, or adds points to an existing design, the report is updated automatically. The complete report can be copied to the clipboard for pasting into a word processing application like Microsoft Word by selecting Edit > Copy from the main menu when the report view is active. The text and graphics are copied using rich text format (RTF) to preserve formatting. The user opens Microsoft Word, selects Paste, and the entire report is copied into a Word document.

The sensitivity table in the Report View allows the user to do "what-if" scenarios with VSP input and output. For the sampling problem shown in Figure 4.12, the sensitivity table shows how sample size changes with changes in the standard deviation and the two decision error rates, alpha and beta. Different sampling goals and sets of assumptions have different variables and parameters in their sensitivity table. The user can change the variables and range of values shown in the sensitivity table by right-clicking anywhere in the report. 

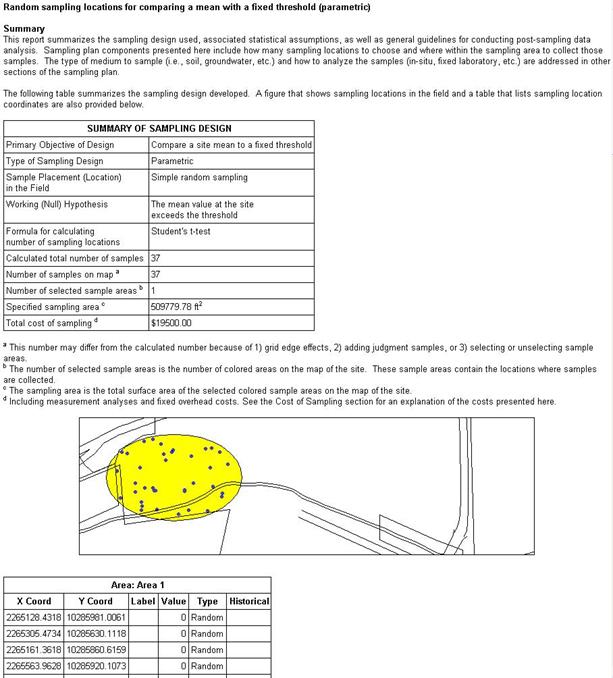
Figure 4.12.   Report View of the Sampling Goal: Compare Average to a Fixed Threshold, Normality Assumed, Ordinary Sampling

A dialog box, as shown in Figure 4.13, is displayed to allow the user to choose which of up to four variables will be displayed in the sensitivity table, along with each variable's starting and ending value, and the step-size. Shown in red are the values the variables will take.

Figure 4.14 shows the sensitivity table that will be included in the Report (View > Report). Displayed in the table can be the number or samples, cost, or both. Certain sampling designs have the option to show parameters other than cost.

The Report changes based on the Sampling Goal selected. Figures 4.15 and 4.16 show portions of the Report for the sampling goal of Sampling within a Building. Shown are the two sampling areas: rooms in yellow are Sampling Room 1; rooms in darker yellow are Sampling Room 2, which is also the Current Room. In Figure 4.16 we also see the detail on the samples placed within the two rooms, along with their actual and relative coordinates, type of sample, and whether the sample is placed on the floor, ceiling, walls, or windows and doors.

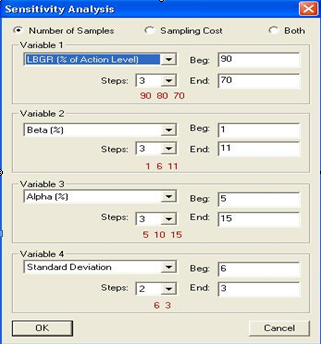
Figure 4.13.   Dialog Box for Changing Variables Displayed, and Range for Variables Shown, in Sensitivity Table in Report View.  Shown here is input dialog for sampling goal of compare average to threshold, normality assumed (parametric), ordinary sampling.

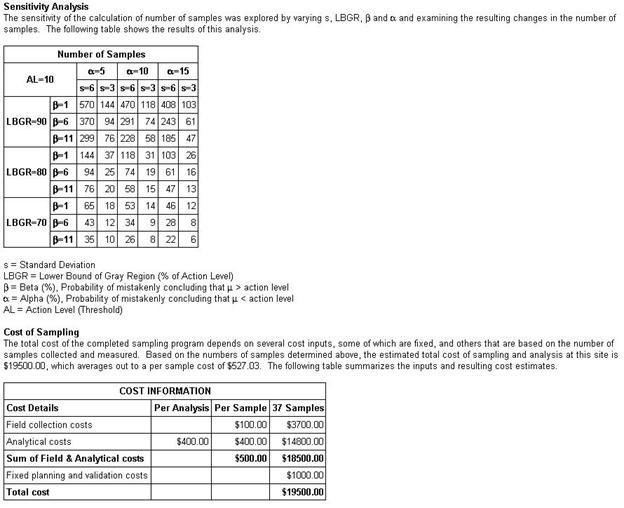
Figure 4.14.   Sensitivity Table for Sampling Goal:  Compare Average to a Fixed Threshold, Normality Assumed, Ordinary Sampling. Cost information shown in bottom of figure.

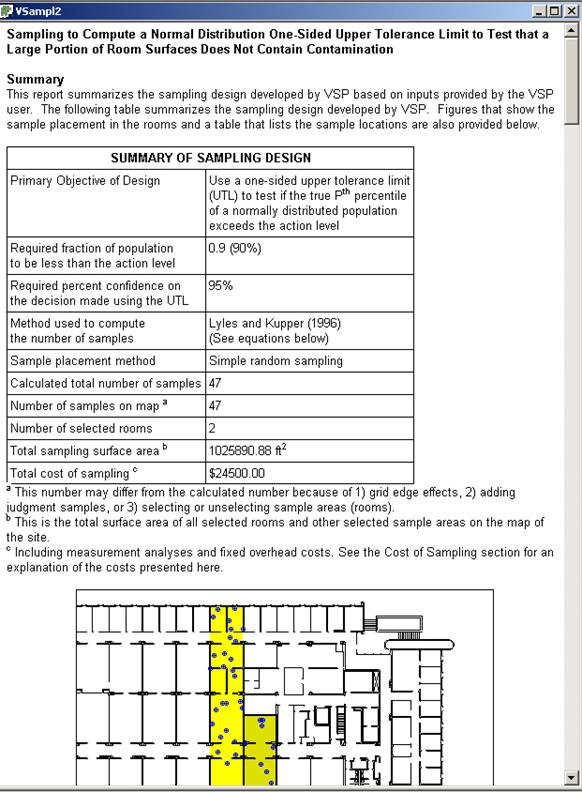
Figure 4.15.   Report View for Sampling within a Building. Shown are summary information for design and location of samples areas selected within the floor plan.

Figure 4.16.   Report View for Sampling within a Building. Shown are current room, and sample information.

4.5 Display of Coordinates

The fourth type of display in VSP is the list of coordinates for each sample point on the map. We can see this display by using the COORDINATE VIEW button on the toolbar, or by selecting Main Menu option View > Coordinates. The x and y coordinates are displayed for each sample point. Also displayed are the sample points label, a value (if entered by the user), the type (e.g., random, systematic, RSS), and a "true/false" indicator of whether or not this sample point is a historical sample (previously taken sample). Coordinates are segregated by Sample Area. These coordinates can be copied and pasted into a spreadsheet or word processing file using Main Menu option Edit > Copy. Figure 4.17 is an example of the Coordinates view. It should also be noted that for modules with a Data Entry tab, some of this information can also be viewed there. Additionally, the analytical modules under Sampling Goals > Find Target Areas and Analyze Survey Results (UXO) have a Data Entry and Analysis tab used for exporting coordinates to be edited outside of VSP (see Chapter 7), and the coordinates are not displayed in the COORDINATE VIEW due to these datasets often being large. If searching for target areas, we don't display the coordinates. See Section 7.2.1 for more information.

Figure 4.17.   Coordinates Display of Sampling Locations

4.6 Multiple Displays

For help during this section, please refer to the VSP Help Topic Window menu commands.

Multiple displays can be brought up on the same screen. Table 4.3 lists the options available under the main menu item Window. 

Table 4.3.   Window Menu Commands

The user can select the QUAD WINDOW button from the toolbar for a quick way to display the Quad Window. Figure 4.18 shows the results of the Quad Window option.

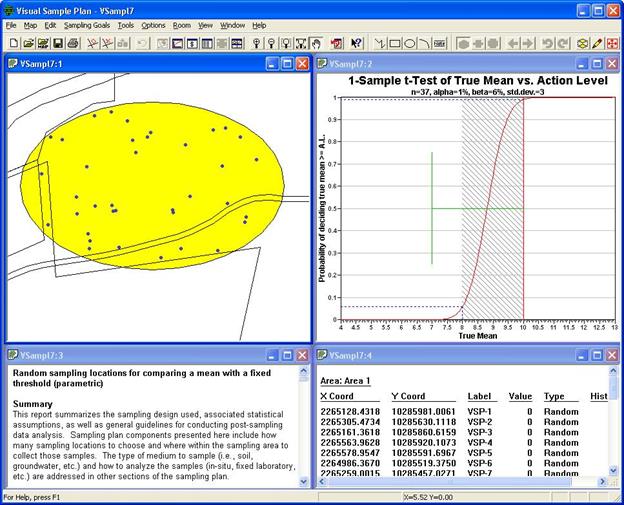
Figure 4.18.   Quad Display of Map, Graph, Report, and Coordinates on Same Screen

To summarize, in Figure 4.19 we show the selection of a Sampling Goal and sample type (Simple Random Sampling), we have entered the DQO inputs into the dialog box, Applied the design to our Sample Area, and displayed the Map, Graph, Report, and Coordinates simultaneously using the Quad Window from the Windows menu.

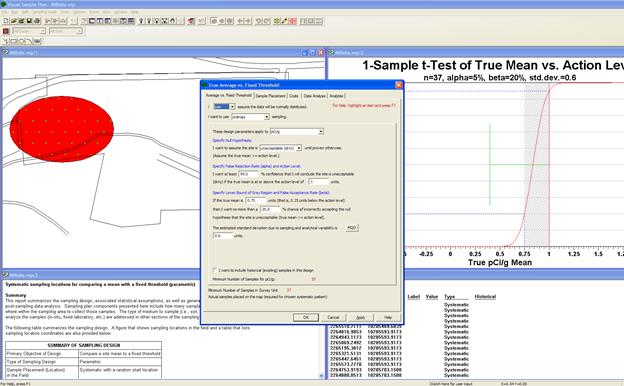
Figure 4.19.   Combined Display of VSP Inputs and Outputs

4.7 Room View

Using View > Room View displays the current room when working with rooms. This is covered in Chapter 6.

4.8 3D View

The 3D view allows for a three-dimensional view of the map. If the project contains rooms or 3D areas, they will be shown with proper perspective height. Figure 4.20 shows a building having many rooms shown in the 3D View.

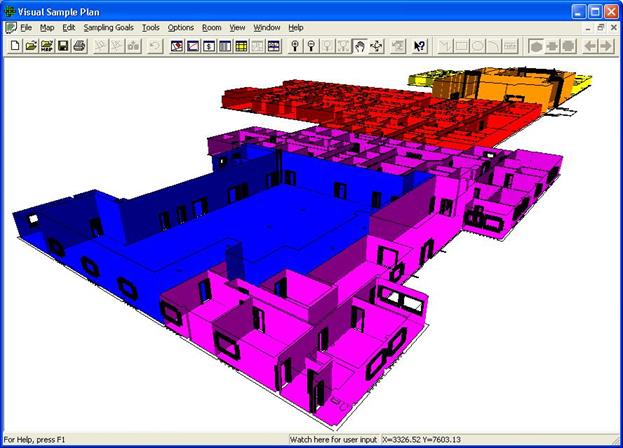
Figure 4.20                 3D View with many rooms

For navigation, the 3D View uses three of the tools used by the Map View (Zoom In, Zoom Out and Pan). It also introduces a new navigation tool: the Rotate / Tilt tool.

When using the Rotate / Tilt tool (View > Rotate on the menu), the cursor becomes a double-ended curved arrow. If you move the cursor to the left edge of view, the tool becomes a Tilt tool. Press and hold the left mouse button while moving the cursor up or down to tilt the view. If you move the cursor away from the left edge of the view, the tool becomes a Rotate tool. Press and hold the left mouse button while moving the cursor around to rotate the view. If the map contains rooms, the view rotates around your point of view (to facilitate navigating through buildings), otherwise the view rotates around the center of the view.

Previous Next

References