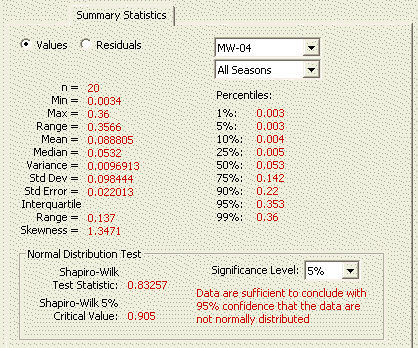
This sub-page of the Data Analysis page displays basic summary statistics computed from the individual trend data values from the Data Entry Sub-page.

Values button |
Show summary statistics for raw data values |
Residuals button |
Show summary statistics for the residuals from the linear regression trend line. |
Location drop-list |
Select location (or all locations) for which to show summary statistics. |
Season drop-list |
Select season (for Seasonal Kendall design) for which to show summary stats. |
\(n\) |
is the number of measurements in a data set |
Min |
is the minimum of the \(n\) data |
Max |
is the maximum of the \(n\) data |
Range |
is the minimum value minus the maximum value, i.e., \( Range = x_{[n]} - x_{[1]} \) |
Mean |
is the arithmetic mean computed as: \( \bar x= \frac{1}{n} \displaystyle\sum\limits_{i=1}^n x_i \) |
Median |
is the 50th percentile of the data set, i.e., the value above which and below which half the data set lies. The sample median is computed from the ordered data (order statistics) \( x_{[1]} \leq x_{[2]} \leq \dotsb \leq x_{[n]} \) as follows: Median = \( x_{[(n+1)/2]} \) if \(n\) is an odd number Median = \( \frac{1}{2} (x_{[n/2]} + x_{[(n+2)/2]}) \) if \(n\) is an even number |
Variance |
is computed as: \( Var = s^2 \) (see below) |
Standard Deviation |
is computed as: \( s = \sqrt{ \frac{1}{n-1} \displaystyle\sum\limits_{i=1}^n (x_i - \bar x)^2} \) |
Standard Error |
is the standard deviation of the estimated mean. It is computed as: \( SE = \frac{s}{ \sqrt{n}} = \sqrt{ \frac{1}{n(n-1)} \displaystyle\sum\limits_{i=1}^n (x_i - \bar x)^2} \) |
Interquartile Range |
is the 75th percentile of the data set minus the 25th percentile of the data set |
Skewness |
Is a measure of the symmetry of the data set. It is computed as: \( SKEW = \frac{ \frac{n}{(n-1)(n-2)} \displaystyle\sum\limits_{i=1}^n (x_i - \bar x)^3}{s^3} \) where \( \bar x \) and s are computed as given above. |
\(P\)th Percentile |
is the value below which \(p\)% of the \(n\) data fall and above which (100 - \(p\))% of the \(n\) data fall. The \(P\)th percentile is computed in VSP by first computing \(k\) = \(p\)(\(n\)+1). If \(k\) is an integer, the \(P\)th percentile is \( x_{[k]} \) , which is the \(K\)th largest of the \(n\) data values. For example, to compute the 50th percentile of a data set of \(n\) = 9 measurements, we have \(p\) = 0.50 and \(k\) = \(p\)(\(n\)+1) = 0.50(10) = 5, which is an integer. Hence, the 50th percentile (the median) is the 5th largest datum, \( x_{[5]} \) . If \(k\) is not an integer, the \(P\)th percentile is obtained by linear interpolation between the two closest order statistics. For example if \(n\) = 11 and \(p\) = 0.70, then \(k\) = \(p\)(\(n\)+1) = 0.70(12) = 8.4, then the 70th percentile is found by linear interpolation between the 8th and 9th largest of the 11 data, i.e., between \( x_{[8]} \) and \( x_{[9]} \). |
Normal Distribution Test |
|
Significance Level |
Choose a 1%, 5%, or 10% significance level for the associated normality test. |
|
VSP conducts a Shapiro-Wilk normality test if there are fewer than 50 selected data values; otherwise a Lilliefors normality test is conducted. |
Conover, W.J. 1999. Practical Nonparametric Statistics, 3rd edition, Wiley, NY.
Gilbert, R.O. 1987. Statistical Methods for Environmental Pollution Monitoring, Wiley, NY.
ProUCL. 2004. ProUCL Version 3.0 User Guide April 2004. Available for download from http://www.epa.gov/nerlesd1/tsc/tsc.htm