Multiple Increment Sampling: Confidence Interval on a Mean

Background Information

The purpose of the Confidence Interval on a Mean option is to calculate the minimum number of samples required to estimate the mean within a pre-specified margin of error at a given confidence level. This option assumes the data will be drawn from an approximately normal distribution or that the number of increments gathered is large enough so that the distribution of sample means is approximately normal.

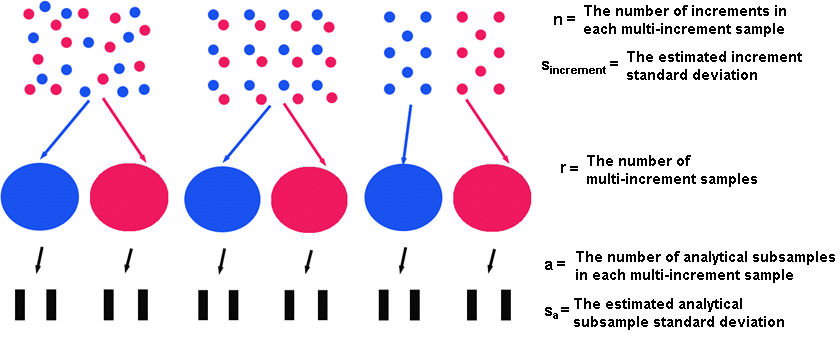
Multiple Increment (MI) sample designs (Composite sample designs) often arise because of the expense associated with analytical tests. A researcher would take $n$ increments and combine them together in $r$ groups (i.e. compositing or mixing soils together into one MI sample) and take measurements of each MI sample to get the average concentration for the combined increments. These measurements on each of the $r$ MI samples are assumed to provide an accurate estimate of the mean concentration as if an average measurement was calculated from each of the individually measured increments. The following diagrams show the MI sampling process with three different methods of placing the increments on the site.

$image\MultInc2.gif$

Equations Used to Calculate Recommended Minimum Number of Samples

The standard equation currently used in VSP to estimate the number of samples ($n$) which should be used to calculate a confidence interval on a mean is shown first. This equation was obtained from (Gilbert, Wilson et al. 2005) and is also provided in the associated help files included with VSP. The equation is

\begin{equation} n = \Big(\frac{t_{1-\alpha, df}}{d}\Big)^2(s_{\text{total}}^2) \end{equation} (1.1)

where $t_{1-\alpha, df}$ describes the associated t-distribution based on $df = n-1$ and $d$ is the maximum desired width of the confidence interval.

The variance component in Equation 1.1 ($s_{\text{total}}^2$) can be represented as

\begin{equation} s_{\text{total}}^2 = s_{\text{sample}}^2 + \frac{s_a^2}{a} \end{equation} (1.2)

if there will be multiple analytical measurements ($a$) performed and there is an estimate for $s_a^2$. These equations are similar to the basic framework for the following equations that are used to calculate the total number of multiple increment samples to gather.

The general difference between Equation 1.1 and Equation 1.3 revolve around the fact that $s_{\text{total}}^2$ is a combination of three possible unknown sample elements. You may know the standard inputs for Equation 1.1 but you are left with how many replicate composite samples, increment samples, and repeated measurements to select ($r$, $n$, $a$) when you know all the other necessary inputs. Also, the $n$ increments included in the multiple increment sample are not measured individually but are combined (through physical mixing) and measurements of the mixture are taken. Some different variance components that could be included in the total variation between composites include

between increment variation
within increment variation
blending variation as the increments are mixed in the composite, and
measurement variation

as described in (Brown and Fisher 1972; Elder, Thompson et al. 1980; Rohlf, Akcakaya et al. 1996). The methods described below will account for between increment variation and subsample measurement variation. It should be explicitly noted that the blending variation is assumed to be very small. If the blending variation is too large the cost advantages of MI sampling will be lost (Hathaway et al. 2008). Thus, the overall variance between composites will be measured as

\begin{equation} s_{\text{total}}^2 = \frac{s_{\text{analytical}}^2}{a}+\frac{s_{\text{increment}}^2}{n} \end{equation} (1.3)

Where $s_{\text{increment}}^2$ would be the same as $s_{\text{sample}}^2$ if each multiple increment sample were formed of $n$ randomly selected increments of the total number of $rn$ increments on the site of interest (See Figure above). If the $n$ increments included in a specific multiple increment sample were not randomly selected from the entire site but selected from a smaller portion of the site (See Figure above) then $s_{\text{increment}}^2 \le s_{\text{sample}}^2$ and $s_{\text{sample}}^2$ could be used as a conservative estimate, if no other estimate of $s_{\text{increment}}^2$ could be obtained. Using equation 1.1 and 1.3 the confidence interval on a mean equation to estimate the necessary number of composites is shown in Equation 1.4.

\begin{equation} r = \frac{t_{1-\alpha, df}^2\Big(\frac{s_{\text{increment}}^2}{n}+\frac{s_a^2}{a}\Big)}{d^2} \end{equation} (1.4)

where

$r$ is the number of multiple increment (MI) samples,

$n$ is the number of increments per MI sample,

$s_{\text{increment}}$ is the estimated standard deviation of the between increment error,

$a$ is the number of analytical subsamples per MI sample,

$s_a$ is the estimated standard deviation of the between increment error,

$d$ is the width of the confidence interval,

$\alpha$ is the probability of rejecting the null hypothesis when the null hypothesis is true,

$df$ is the degrees of freedom for the t-distribution which is $r-1$, and

$t_{1-\alpha, df}$ is the value of the t-distribution such that the proportion of the distribution less than $t_{1-\alpha, df}$ is $1- \alpha$,

Method of calculating the optimal number of MI samples, Increments, and analytical subsamples ($r$, $a$, $n$)

When $a$ and $n$ are fixed in the design dialog, Equation 1.4 is used to identify the number of MI samples ($r$) to gather. If $a$ and $n$ are not fixed in the design dialog, then VSP uses one of the following two methods described by Rohlf, Akcakaya et al. (1996).

Method 1

If the option to find the optimal sampling plan for a fixed cost is selected the following iteration is used where $C$ represents the cost associated with its respective label.

1. Calculate the ratio

\begin{equation} \sqrt{\frac{s_a^2C_{\text{sample collection and combination}}}{s_{\text{increment}}^2C_{\text{Individual Measurement}}}} \end{equation} (1.5)

2. For integer values of $a$ and $n$ where $n \ge a/\text{ratio}$ compute

\begin{equation} r = \frac{C_{\text{total}}}{(nC_{\text{sample collection and combination}}+aC_{\text{Individual Measurement}})} \end{equation} (1.6)

requiring that $r \ge 2$.

3. Now for all good combinations of $r$, $a$, and $n$, calculate the smallest confidence interval by solving for $d$ from Equation 1.4

4. Finally compute that actual total cost using

\begin{equation} \text{Total Cost} (C_{\text{total}}) = r(nC_{\text{sample collection and combination}}+aC_{\text{Individual Measurement}}) \end{equation} (1.7)

and summarize the top five confidence interval options with their associated $r$, $n$, $a$, and total cost.

Method 2

If the option to find the minimum cost for a desired width of confidence interval is selected the following iteration is used where $C$ represents the cost associated with its respective label.

1. Calculate the ratio

\begin{equation} \sqrt{\frac{s_a^2C_{\text{sample collection and combination}}}{s_{\text{increment}}^2C_{\text{Individual Measurement}}}} \end{equation} (1.8)

2. For integer values of $a$ and $n$ where $n \ge a/\text{ratio}$ compute the desired r from Equation 1.4. This is done iteratively because $df$ is dependant on $r$. This approach is detailed in Gilbert, Wilson et al. (2005). VSP requires that $r \ge 2$.

3. For each plausible combination of $r$, $a$, and $n$, calculate $C_{\text{total}}$ from Equation 1.7.

4. Finally compute the actual confidence interval that could be obtained and summarize the top five least expensive options with their associated $r$, $n$, $a$, and $d$.

Statistical Assumptions

The assumptions associated with the formulas for computing the number of samples are:

1. The MI sample mean is normally distributed (this happens if the data are roughly symmetric or the total number of increments is more than 30; for extremely skewed data sets, additional samples may be required for the sample mean to be normally distributed).

2. The standard deviation estimates, $s_{\text{increment}}$ and $s_a$,are reasonable and representative of the populations being sampled.

3. The population values are not spatially or temporally correlated.

4. The sampling locations will be selected probabilistically.

5. The process of mixing increments in together in each MI sample is very good.

6. The number of MI samples must be two or greater.

The first three assumptions should be assessed in a post data collection analysis. The fourth assumption is valid because the gridded sample locations were selected based on a random start. It is recommended that the fifth assumption be examined during the study or in a previous study.

References:

Brown, G. H. and N. I. Fisher. 1972. Subsampling a Mixture of Sampled Material. Technometrics 14(3): 663-&.

Elder, R. S., W. O. Thompson, et al. 1980. Properties of Composite Sampling Procedures. Technometrics 22(2): 179-186.

Gilbert, R., J. Wilson, et al. 2005. Technical Documentation and Verification for the Buildings Module in the Visual Sample Plan (VSP) Software. Pacific Northwest National Laboratory, Richland, Washington.

Gilbert, R. O. 1987. Statistical methods for environmental pollution monitoring. New York, Van Nostrand Reinhold Co.

Guenther, W. C. 1982. Normal Theory Sample-Size Formulas for Some Non-Normal Distributions. Communications in Statistics Part B-Simulation and Computation 11(6): 727-732.

Hathaway JE, G Schaalje, RO Gilbert, BA Pulsipher, and BD Matzke. 2008. Determining the Optimum Number of Increments in Composite Sampling. Environmental and Ecological Statistics. [Accepted]

Owen, D. B. 1962. Handbook of statistical tables. Reading, Mass., Addison-Wesley.

Rohlf, F. J., H. R. Akcakaya, et al. 1996. Optimizing composite sampling protocols. Environmental Science & Technology 30(10): 2899-2905.